2019. 8. 5. 16:38ㆍ프로그래밍언어/Java&Servlet
네이버의 d2 블로그에 Java Hashmap 동작에 대해 아주 상세히 설명한 자료가 있어 참조해보았다. 해시맵에 대해 아주 상세하게 작성한 글이라 알아두면 아주 좋을 것 같다.
참조 : https://d2.naver.com/helloworld/831311
Java HashMap은 어떻게 동작하는가?
이 글은 Java 7과 Java 8을 기준으로 HashMap이 어떻게 구현되어 있는지 설명합니다. HashMap 자체의 소스 코드는 Oracle JDK나 OpenJDK나 같기 때문에, 이 글이 설명하는 HashMap 구현 방식은 Oracle JDK와 OpenJDK 둘 모두에 해당한다고 할 수 있습니다. Java가 아닌 다른 언어를 주로 사용하는 개발자라 하더라도, Java의 HashMap이 현재 어떻게 구현되어 있고, 어떻게 발전되었는지 알면 라이브러리나 프레임워크 구현에 대한 혜안을 얻을 수 있을 것이라고 기대합니다.
HashMap은 Java Collections Framework에 속한 구현체 클래스입니다. Java Collections Framework는 1998년 12월에 발표한 Java 2에서 정식으로 선보였습니다. Map 인터페이스 자체는 Java 5에서 Generic이 적용된 것 외에 처음 선보인 이후 변화가 없지만, HashMap 구현체는 성능을 향상시키기 위해 지속적으로 변화해 왔습니다.
이 글에서는 어떤 방식으로 HashMap 구현체의 성능을 향상시켰는지 소개합니다. 구체적으로 다루는 내용은 Amortized Constant Time을 위하여 어떻게 해시 충돌(hash collision) 가능성을 줄이고 있는가에 대한 것입니다.
HashMap과 HashTable
이 글에서 말하는 HashMap과 HashTable은 Java의 API 이름이다. HashTable이란 JDK 1.0부터 있던 Java의 API이고, HashMap은 Java 2에서 처음 선보인 Java Collections Framework에 속한 API다. HashTable 또한 Map 인터페이스를 구현하고 있기 때문에 HashMap과 HashTable이 제공하는 기능은 같다. 다만 HashMap은 보조 해시 함수(Additional Hash Function)를 사용하기 때문에 보조 해시 함수를 사용하지 않는 HashTable에 비하여 해시 충돌(hash collision)이 덜 발생할 수 있어 상대으로 성능상 이점이 있다. 보조 해시 함수가 아니더라도, HashTable 구현에는 거의 변화가 없는 반면, HashMap은 지속적으로 개선되고 있다. HashTable의 현재 가치는 JRE 1.0, JRE 1.1 환경을 대상으로 구현한 Java 애플리케이션이 잘 동작할 수 있도록 하위 호환성을 제공하는 것에 있기 때문에, 이 둘 사이에 성능과 기능을 비교하는 것은 큰 의미가 없다고 할 수 있다.
HashMap과 HashTable을 정의한다면, '키에 대한 해시 값을 사용하여 값을 저장하고 조회하며, 키-값 쌍의 개수에 따라 동적으로 크기가 증가하는 associate array'라고 할 수 있다. 이 associate array를 지칭하는 다른 용어가 있는데, 대표적으로 Map, Dictionary, Symbol Table 등이다.
예제 1 HashTable과 HashMap의 선언부
associative array를 지칭하기 위하여 HashTable에서는 Dictionary라는 이름을 사용하고, HashMap에서는 그 명칭이 그대로 말하듯이 Map이라는 용어를 사용하고 있다.
map(또는 mapping)은 원래 수학 함수에서의 대응 관계를 지칭하는 용어로, 경우에 따라서는 함수 자체를 의미하기도 한다. 즉 HashMap이란 이름에서 알 수 있듯이, HashMap은 키 집합인 정의역과 값 집합인 공역의 대응에 해시 함수를 이용한다.

그림 1 함수에서의 사상(map)
해시 분포와 해시 충돌
동일하지 않은 어떤 객체 X와 Y가 있을 때, 즉 X.equals(Y)가 '거짓'일 때 X.hashCode() != Y.hashCode()가 같지 않다면, 이때 사용하는 해시 함수는 완전한 해시 함수(perfect hash functions)라고 한다(

: S는 모든 객체의 집합, h는 해시 함수).
Boolean같이 서로 구별되는 객체의 종류가 적거나, Integer, Long, Double 같은 Number 객체는 객체가 나타내려는 값 자체를 해시 값으로 사용할 수 있기 때문에 완전한 해시 함수 대상으로 삼을 수 있다. 하지만 String이나 POJO(plain old java object)에 대하여 완전한 해시 함수를 제작하는 것은 사실상 불가능하다.
적은 연산만으로 빠르게 동작할 수 있는 완전한 해시 함수가 있다고 하더라도, 그것을 HashMap에서 사용할 수 있는 것은 아니다. HashMap은 기본적으로 각 객체의 hashCode() 메서드가 반환하는 값을 사용하는 데, 결과 자료형은 int다. 32비트 정수 자료형으로는 완전한 자료 해시 함수를 만들 수 없다. 논리적으로 생성 가능한 객체의 수가 232보다 많을 수 있기 때문이며, 또한 모든 HashMap 객체에서 O(1)을 보장하기 위해 랜덤 접근이 가능하게 하려면 원소가 232인 배열을 모든 HashMap이 가지고 있어야 하기 때문이다.
따라서 HashMap을 비롯한 많은 해시 함수를 이용하는 associative array 구현체에서는 메모리를 절약하기 위하여 실제 해시 함수의 표현 정수 범위

보다 작은 M개의 원소가 있는 배열만을 사용한다. 따라서 다음과 같이 객체에 대한 해시 코드의 나머지 값을 해시 버킷 인덱스 값으로 사용한다.
예제 2 해시를 사용하는 associative array 구현체에서 저장/조회할 해시 버킷을 계산하는 방법
이 코드와 같은 방식을 사용하면, 서로 다른 해시 코드를 가지는 서로 다른 객체가 1/M의 확률로 같은 해시 버킷을 사용하게 된다. 이는 해시 함수가 얼마나 해시 충돌을 회피하도록 잘 구현되었느냐에 상관없이 발생할 수 있는 또 다른 종류의 해시 충돌이다. 이렇게 해시 충돌이 발생하더라도 키-값 쌍 데이터를 잘 저장하고 조회할 수 있게 하는 방식에는 대표적으로 두 가지가 있는데, 하나는 Open Addressing이고, 다른 하나는 Separate Chaining이다. 이 둘 외에도 해시 충돌을 해결하기 위한 다양한 자료 구조가 있지만, 거의 모두 이 둘을 응용한 것이라고 할 수 있다.
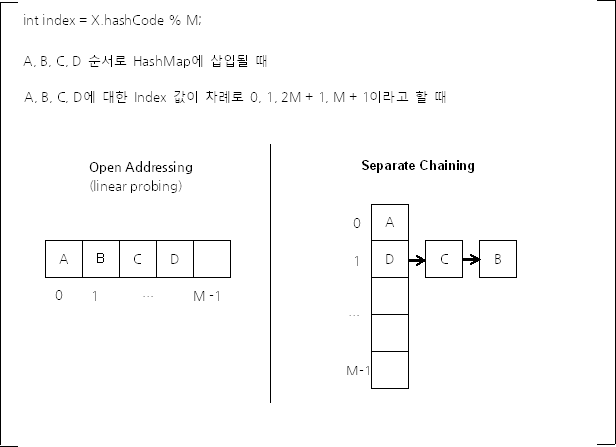
그림 2 Open Addressing과 Separate Chaining 구조
Open Addressing은 데이터를 삽입하려는 해시 버킷이 이미 사용 중인 경우 다른 해시 버킷에 해당 데이터를 삽입하는 방식이다. 데이터를 저장/조회할 해시 버킷을 찾을 때에는 Linear Probing, Quadratic Probing 등의 방법을 사용한다.
Separate Chaining에서 각 배열의 인자는 인덱스가 같은 해시 버킷을 연결한 링크드 리스트의 첫 부분(head)이다.
둘 모두 Worst Case O(M)이다. 하지만 Open Addressing은 연속된 공간에 데이터를 저장하기 때문에 Separate Chaining에 비하여 캐시 효율이 높다. 따라서 데이터 개수가 충분히 적다면 Open Addressing이 Separate Chaining보다 더 성능이 좋다. 하지만 배열의 크기가 커질수록(M 값이 커질수록) 캐시 효율이라는 Open Addressing의 장점은 사라진다. 배열의 크기가 커지면, L1, L2 캐시 적중률(hit ratio)이 낮아지기 때문이다.
Java HashMap에서 사용하는 방식은 Separate Channing이다. Open Addressing은 데이터를 삭제할 때 처리가 효율적이기 어려운데, HashMap에서 remove() 메서드는 매우 빈번하게 호출될 수 있기 때문이다. 게다가 HashMap에 저장된 키-값 쌍 개수가 일정 개수 이상으로 많아지면, 일반적으로 Open Addressing은 Separate Chaining보다 느리다. Open Addressing의 경우 해시 버킷을 채운 밀도가 높아질수록 Worst Case 발생 빈도가 더 높아지기 때문이다. 반면 Separate Chaining 방식의 경우 해시 충돌이 잘 발생하지 않도록 '조정'할 수 있다면 Worst Case 또는 Worst Case에 가까운 일이 발생하는 것을 줄일 수 있다(여기에 대해서는 "보조 해시 함수"에서 설명하겠다).
예제 3 Java 7에서의 해시 버킷 관련 구현
Separate Chaining 방식을 사용하기 때문에, Java 7에서의 put() 메서드 구현은 예제 4에서 보는 것과 같다.
예제 4 put() 메서드 구현
그러나 Java 8에서는 예제 4에서 볼 수 있는 것보다 더 발전된 방식을 사용한다.
Java 8 HashMap에서의 Separate Chaining
Java 2부터 Java 7까지의 HashMap에서 Separate Chaining 구현 코드는 조금씩 다르지만, 구현 알고리즘 자체는 같았다. 만약 객체의 해시 함수 값이 균등 분포(uniform distribution) 상태라고 할 때, get() 메서드 호출에 대한 기댓값은

이다. 그러나 Java 8에서는 이보다 더 나은
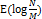
을 보장한다. 데이터의 개수가 많아지면, Separate Chaining에서 링크드 리스트 대신 트리를 사용하기 때문이다.
데이터의 개수가 많아지면

과

의 차이는 무시할 수 없다. 게다가 실제 해시 값은 균등 분포가 아닐뿐더러, 설사 균등 분포를 따른다고 하더라도 birthday problem이 설명하듯 일부 해시 버킷 몇 개에 데이터가 집중될 수 있다. 그래서 데이터의 개수가 일정 이상일 때에는 링크드 리스트 대신 트리를 사용하는 것이 성능상 이점이 있다.
링크드 리스트를 사용할 것인가 트리를 사용할 것인가에 대한 기준은 하나의 해시 버킷에 할당된 키-값 쌍의 개수이다. 예제 5에서 보듯 Java 8 HashMap에서는 상수 형태로 기준을 정하고 있다. 즉 하나의 해시 버킷에 8개의 키-값 쌍이 모이면 링크드 리스트를 트리로 변경한다. 만약 해당 버킷에 있는 데이터를 삭제하여 개수가 6개에 이르면 다시 링크드 리스트로 변경한다. 트리는 링크드 리스트보다 메모리 사용량이 많고, 데이터의 개수가 적을 때 트리와 링크드 리스트의 Worst Case 수행 시간 차이 비교는 의미가 없기 때문이다. 8과 6으로 2 이상의 차이를 둔 것은, 만약 차이가 1이라면 어떤 한 키-값 쌍이 반복되어 삽입/삭제되는 경우 불필요하게 트리와 링크드 리스트를 변경하는 일이 반복되어 성능 저하가 발생할 수 있기 때문이다.
예제 5 Java 8 HashMap의 TREEIFY_THRESHOLD와 UNTREEIFY_THRESHOLD
Java 8 HashMap에서는 Entry 클래스 대신 Node 클래스를 사용한다. Node 클래스 자체는 사실상 Java 7의 Entry 클래스와 내용이 같지만, 링크드 리스트 대신 트리를 사용할 수 있도록 하위 클래스인 TreeNode가 있다는 것이 Java 7 HashMap과 다르다.
이때 사용하는 트리는 Red-Black Tree인데, Java Collections Framework의 TreeMap과 구현이 거의 같다. 트리 순회 시 사용하는 대소 판단 기준은 해시 함수 값이다. 해시 값을 대소 판단 기준으로 사용하면 Total Ordering에 문제가 생기는데, Java 8 HashMap에서는 이를 tieBreakOrder() 메서드로 해결한다.
예제 6 Java 8 HashMap의 Node 클래스
해시 버킷 동적 확장
해시 버킷의 개수가 적다면 메모리 사용을 아낄 수 있지만 해시 충돌로 인해 성능상 손실이 발생한다. 그래서 HashMap은 키-값 쌍 데이터 개수가 일정 개수 이상이 되면, 해시 버킷의 개수를 두 배로 늘린다. 이렇게 해시 버킷 개수를 늘리면

값도 작아져, 해시 충돌로 인한 성능 손실 문제를 어느 정도 해결할 수 있다.
해시 버킷 개수의 기본값은 16이고, 데이터의 개수가 임계점에 이를 때마다 해시 버킷 개수의 크기를 두 배씩 증가시킨다. 버킷의 최대 개수는 230개다. 그런데 이렇게 버킷 개수가 두 배로 증가할 때마다, 모든 키-값 데이터를 읽어 새로운 Separate Chaining을 구성해야 하는 문제가 있다. HashMap 생성자의 인자로 초기 해시 버킷 개수를 지정할 수 있으므로, 해당 HashMap 객체에 저장될 데이터의 개수가 어느 정도인지 예측 가능한 경우에는 이를 생성자의 인자로 지정하면 불필요하게 Separate Chaining을 재구성하지 않게 할 수 있다.
예제 7 Java 7 HashMap에서의 해시 버킷 확장
해시 버킷 크기를 두 배로 확장하는 임계점은 현재의 데이터 개수가 'load factor * 현재의 해시 버킷 개수'에 이를 때이다. 이 load factor는 0.75 즉 3/4이다. 이 load factor 또한 HashMap의 생성자에서 지정할 수 있다.
임계점에 이르면 항상 해시 버킷 크기를 두 배로 확장하기 때문에, N개의 데이터를 삽입했을 때의 키-값 쌍 접근 횟수는 다음과 같이 분석할 수 있다.

즉 기본 생성자로로 생성한 HashMap을 이용하여 많은 양의 데이터를 삽입할 때에는, 최적의 해시 버킷 개수를 지정한 것보다 약 2.5배 많이 키-값 쌍 데이터에 접근해야 한다. 이는 곧 수행 시간이 2.5배 길어진다고 할 수 있다. 따라서 성능을 높이려면, HashMap 객체를 생성할 때 적정한 해시 버킷 개수를 지정해야 한다.
그런데 이렇게 해시 버킷 크기를 두 배로 확장하는 것에는 결정적인 문제가 있다. 해시 버킷의 개수 M이 2a 형태가 되기 때문에, index = X.hashCode() % M을 계산할 때 X.hashCode()의 하위 a개의 비트만 사용하게 된다는 것이다. 즉 해시 함수가 32비트 영역을 고르게 사용하도록 만들었다 하더라도 해시 값을 2의 승수로 나누면 해시 충돌이 쉽게 발생할 수 있다.
이 때문에 보조 해시 함수가 필요하다.
보조 해시 함수
index = X.hashCode() % M을 계산할 때 사용하는 M 값은 소수일 때 index 값 분포가 가장 균등할 수 있다. 그러나 M 값이 소수가 아니기 때문에 별도의 보조 해시 함수를 이용하여 index 값 분포가 가급적 균등할 수 있도록 해야 한다.
보조 해시 함수(supplement hash function)의 목적은 '키'의 해시 값을 변형하여, 해시 충돌 가능성을 줄이는 것이다. 이 보조 해시 함수는 JDK 1.4에 처음 등장했다. Java 5 ~ Java 7은 같은 방식의 보조 해시 함수를 사용하고, Java 8부터는 다시 새로운 방식의 보조 해시 함수를 사용하고 있다.
예제 8 Java 7 HashMap에서의 보조 해시 함수
그런데 Java 8에서는 Java 7보다 훨씬 더 단순한 형태의 보조 해시 함수를 사용한다.
예제 9 Java 8 HashMap에서의 보조 해시 함수
예제 9에서 볼 수 있는 것처럼, Java 8 HashMap 보조 해시 함수는 상위 16비트 값을 XOR 연산하는 매우 단순한 형태의 보조 해시 함수를 사용한다. 이유로는 두 가지가 있는데, 첫 번째는 Java 8에서는 해시 충돌이 많이 발생하면 링크드 리스트 대신 트리를 사용하므로 해시 충돌 시 발생할 수 있는 성능 문제가 완화되었기 때문이다. 두 번째로는 최근의 해시 함수는 균등 분포가 잘 되게 만들어지는 경향이 많아, Java 7까지 사용했던 보조 해시 함수의 효과가 크지 않기 때문이다. 두 번째 이유가 좀 더 결정적인 원인이 되어 Java 8에서는 보조 해시 함수의 구현을 바꾸었다.
개념상 해시 버킷 인덱스를 계산할 때에는 index = X.hashCode() % M처럼 나머지 연산을 사용하는 것이 맞지만, M값이 2a일 때는 해시 함수의 하위 a비트 만을 취한 것과 값이 같다. 따라서 나머지 연산 대신 '1 << a – 1' 와 비트 논리곱(AND, &) 연산을 사용하면 수행이 훨씬 더 빠르다.
String 객체에 대한 해시 함수
String 객체에 대한 해시 함수 수행 시간은 문자열 길이에 비례한다.
때문에 JDK 1.1에서는 String 객체에 대해서 빠르게 해시 함수를 수행하기 위해, 일정 간격의 문자에 대한 해시를 누적한 값을 문자열에 대한 해시 함수로 사용했다.
예제 10 JDK 1.1에서의 String 클래스 해시 함수
예제 10에서 볼 수 있듯이 모든 문자에 대한 해시 함수를 계산하는 게 아니라, 문자열의 길이가 16을 넘으면 최소 하나의 문자를 건너가며 해시 함수를 계산했다.
그러나 이런 방식은 심각한 문제를 야기했다. 웹상의 URL은 길이가 수십 글자에 이르면서 앞 부분은 동일하게 구성되는 경우가 많다. 이 경우 서로 다른 URL의 해시 값이 같아지는 빈도가 매우 높아질 수 있다는 문제가 있다. 따라서 이런 방식은 곧 폐기되었고, 예제 11에서 보는 방식을 현재의 Java 8까지도 계속 사용하고 있다.
예제 11 Java String 클래스 해시 함수
예제 11은 Horner's method를 구현한 것이다. Horner's method는 다항식을 계산하기 쉽도록 단항식으로 이루어진 식으로 표현하는 것이다. 즉 예제 11에서 계산하고자 하는 해시 값 h는 다음과 같다.



이렇게 단항식을 재귀적으로 사용하여 다항식 연산을 표현할 수 있다.
String 객체 해시 함수에서 31을 사용하는 이유는, 31이 소수이며 또한 어떤 수에 31을 곱하는 것은 빠르게 계산할 수 있기 때문이다. 31N=32N-N인데, 32는 25이니 어떤 수에 대한 32를 곱한 값은 shift 연산으로 쉽게 구현할 수 있다. 따라서 N에 31을 곱한 값은, (N << 5) – N과 같다. 31을 곱하는 연산은 이렇게 최적화된 머신 코드로 생성할 수 있기 때문에, String 클래스에서 해시 값을 계산할 때에는 31을 승수로 사용한다.
Java 7에서 String 객체에 대한 별도의 해시 함수
JDK 7u6부터 JDK 7u25까지는 HashMap에 저장된 키-값 쌍이 일정 개수 이상이면 String 객체에 한하여 별도의 해시 함수를 사용할 수 있게 하는 기능이 있다. 이 기능은 JDK 7u40부터는 삭제되었고, 당연히 Java 8에도 해당 기능은 없다. 여기서 말하는 '일정 개수 이상'이나 '별도의 해시 함수 사용 여부 지정'은 JVM을 가동할 때 옵션으로 지정할 수 있다.
예제 12 Java 7의 String에 대한 hash32() 메서드
JDK 7u6부터 JDK 7u25까지는 jdk.map.althashing.threshold 옵션을 지정하면, HashMap에 저장된 키-값 쌍이 일정 개수 이상일 때 String 객체에 String 클래스의 hashCode() 메서드 대신 sun.misc.Hashing.stringHash32() 메서드를 사용할 수 있게 했다. sun.misc.Hashing.stringHash32() 메서드는 String 클래스의 hash32() 메서드를 호출하게 한 것이고, hash32() 메서드는 MurMur 해시를 구현한 것이다. 이 MurMur 해시를 이용하여 String 객체에 대한 해시 충돌을 매우 낮출 수 있었다고 한다.
그러나 부작용도 있다. MurMur 해시는 hash seed를 필요로 하는데, 이를 위한 것이 sun.misc.Hashing.randomHashSeed() 메서드다. 이 메서드에서는 Random.nextInt() 메서드를 사용한다. Random.nextInt() 메서드는 compare and swap 연산(이하 CAS 연산)을 사용하는 AtomicLong을 사용하는데, CAS 연산은 코어가 많을수록 성능이 떨어진다. 즉 JDK 7u6부터 등장한 String 객체에 대한 별도의 해시 함수는 멀티 코어 환경에서는 성능이 하락했고, 이런 문제로 인해 JDK 7u40부터는 해당 기능을 사용하지 않는다. 당연히 Java 8도 사용하지 않는다.
'프로그래밍언어 > Java&Servlet' 카테고리의 다른 글
| Java - 중첩이 많은 Stream 처리 Tip ! (0) | 2020.04.21 |
|---|---|
| Java - CopyOnWriteArraySet 클래스 (0) | 2019.12.19 |
| Java - Garbage Collection(GC,가비지 컬렉션) 란? (1) | 2019.07.29 |
| Java - JVM이란? JVM 메모리 구조 (1) | 2019.07.29 |
| Eclipse - Archive for required library 해결방법 (0) | 2019.06.18 |